HYPERBOLE

HYPERBOLA

The hyperbola is centered on a point (h, k), which is the "center" of the hyperbola. The point on each branch closest to the center is that branch's "vertex". The vertices are some fixed distance a from the center. The line going from one vertex, through the center, and ending at the other vertex is called the "transverse" axis. The "foci" of an hyperbola are "inside" each branch, and each focus is located some fixed distance c from the center. (This means that a < c for hyperbolas.) The values of a and c will vary from one hyperbola to another, but they will be fixed values for any given hyperbola.

Did you know that the orbit of a spacecraft can sometimes be a hyperbola?

A spacecraft can use the gravity of a planet to alter its path and propel it at high speed away from the planet and back out into space using a technique called "gravitational slingshot".

If this happens, then the path of the spacecraft is a hyperbola.

 

Definition

A hyperbola is a curve where the distances of any point from:

• a fixed point (the focus), and
• a fixed straight line (the directrix) are always in the same ratio.

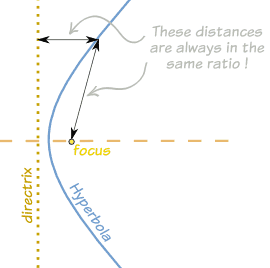
This ratio is called the ecentricity, and for a hyperbola it is always greater than 1.

The hyperbola is an open curve (has no ends).

But that isn't the full story! Because a hyperbola is actually two separate curves in mirror image like this:

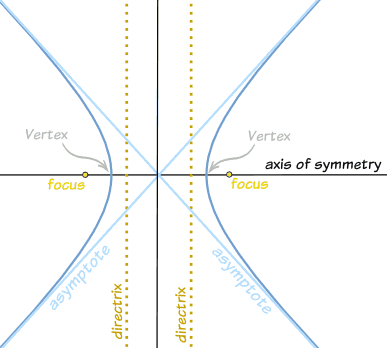
On the diagram you can see:

• a directrix and a focus (one on each side)
• an axis of symmetry (that goes through each focus, at right angles to the directrix)
• two vertices (where each curve makes its sharpest turn)

The "asymptotes" (shown on the diagram) are not part of the hyperbola, but show where the curve would go if continued indefinitely in each of the four directions.

And, strictly speaking, there is also another axis of symmetry that reflects the two separate curves of the hyperbola.

Conic Section You can also get a hyperbola when you slice through a cone. The slice must be steeper than that for a parabola, but does not have to be parallel to the cone's axis for the hyperbola to be symmetrical. So the hyperbola is a conic cection (a section of a cone).

Equation

By placing a hyperbola on an x-y graph (centered over the x-axis and y-axis), the equation of the curve is:

x²/a² − y²/b² = 1

Also: One vertex is at (a, 0), and the other is at (−a, 0) The asymptotes are the straight lines: y = (b/a)x y = −(b/a)x And the equation is also similar to the equation of the ellipse: x2/a2 + y2/b2 = 1, except for a "−" instead of a "+")

Eccentricity

We already mentioned the eccentricity  (usually shown as the letter e), it shows how "uncurvy" (varying from being a circle) the hyperbola is.

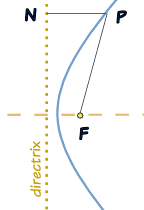
On this diagram:

• P is a point on the curve,
• F is the focus and
• N is the point on the directrix so that PN is perpendicular to the directrix.

The ratio PF/PN is the eccentricity of the hyperbola (for a hyperbola the eccentricity is always greater than 1).

It can also given by the formula:

e =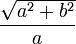

Using "a" and "b" from the diagram above. 

Latus Rectum

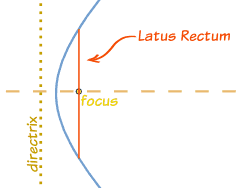The Latus Rectum is the line through the focus and parallel to the directrix. The length of the Latus Rectum is 2b2/a.

reference

http://www.purplemath.com/modules/hyperbola.htm

http://www.mathsisfun.com/geometry/hyperbola.html